|
3)
- Le confinement magnétique
(p 1
- 2 - 3
- 4 )
| Comment
rassembler des particules qui n'ont à priori aucune raison de vouloir rester
ensemble ? Dans le soleil, la gravité s'en charge. Sur Terre, on utilise des
champs magnétiques puissants. |
a)
les trajectoires des particules
Le confinement du plasma dans un tokamak
est basé sur la propriété qu'ont les particules chargées de décrire une
trajectoire en hélice autour d'une ligne de champ magnétique. Regardez le mouvement d'une particule
chargée autour d'une ligne de champ magnétique droite.
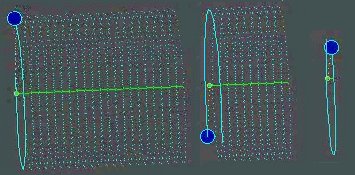
 Voir
le film "trajectoire droite" (mpg, 493 ko)
La
particule, figurée en bleu, décrit une hélice autour de la ligne de champ,
que suit le centre-guide de la trajectoire, matérialisé en vert.
Le
rayon de giration de la particule, appelé rayon de Larmor
 , dépend de
l'intensité du champ magnétique, de la masse et la charge de la particule, et
de son énergie.
Plus le champ magnétique est puissant, plus le rayon de Larmor est faible, la
particule restant "scotchée" au voisinage de la ligne de champ. De
plus, les électrons, beaucoup plus légers que les ions, ont un rayon de Larmor
nettement plus faible à même énergie. Enfin, les particules très
énergétiques ont un rayon de Larmor plus élevé que les particules à faible
énergie, et sont donc plus difficiles à confiner. Le rayon de Larmor
peut varier typiquement entre des millimètres pour des particules peu
énergétiques avec un champ magnétique intense et des dizaines de centimètres
pour des particules très énergétiques.
L'astuce
consiste alors à refermer la ligne de champ sur elle-même pour piéger la
particule, comme vous pouvez le voir ci-dessous.
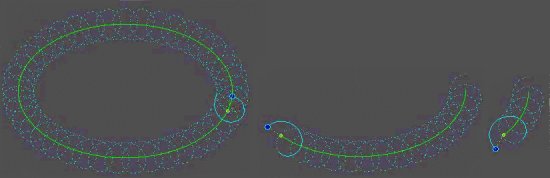
Voir
le film "trajectoire cylindrique" (mpg, 750 ko)
 |
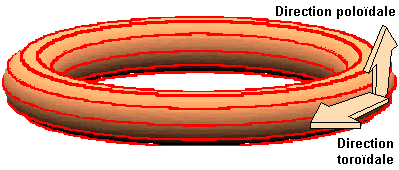On
se trouve alors dans une configuration où la direction du champ magnétique est
purement toroïdale.
|
 |
Malheureusement,
sur une simple trajectoire circulaire de ce type, la particule subit une
lente dérive transverse, liée au gradient de champ magnétique et à la force
centrifuge, et dont la direction dépend du signe de sa charge. Par exemple,
les ions vont dériver vers
le haut (comme illustré sur le schéma ci-contre) et les électrons vers le bas.
|
|
Pour
compenser cet effet, l'idée est alors de stabiliser la configuration en
ajoutant une composante poloïdale au champ magnétique toroïdal. C'est la
configuration magnétique utilisée dans les tokamak . Les lignes de champ
deviennent des hélices s'enroulant autour de surfaces toriques emboîtées,
dites surfaces magnétiques.
|
 |
|
La
particule passe alors la moitié de son temps la tête en haut, où la
dérive verticale, que l'on suppose vers le haut par exemple comme sur
l'exemple ci-dessous, l'éloigne de la surface magnétique, et l'autre
moitié la tête en bas, où la dérive verticale la rapproche de la
surface magnétique. L'effet de dérive est alors en moyenne compensé.
|
 |
|
Particule suivant une ligne
de champ en hélice
|
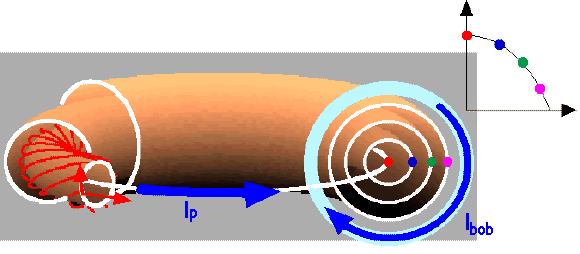
Dans
un tokamak, le champ magnétique toroïdal est engendré par des bobinages
extérieurs, tandis que le champ magnétique poloïdal est induit
par un courant circulant
toroïdalement dans le plasma. Ce courant est lui-même généré par effet
transformateur, à partir d'un circuit primaire dont le le
secondaire est le plasma. Tore Supra possède la particularité d'être
équipé d'aimants supraconducteurs, qui lui permettent d'assurer un champ
toroïdal permanent (les machines équipées d'aimants classiques sont
limitées en durée par l'échauffement des bobines en cuivre). La durée
de la décharge est alors limitée par la capacité du circuit primaire
générant le courant plasma induisant le champ poloïdal.
|
On
appelle facteur de sécurité le pas de l'hélice sur chaque surface magnétique
(c'est à dire le nombre grands tours toroïdaux nécessaires pour effectuer 1
petit tour poloïdal ). Dans une configuration tokamak, ce facteur de sécurité
varie typiquement de 1 au centre du plasma à quelques unités au bord. Il est
à noter que, dans le cas général, si on suit la ligne de champ, elle va
décrire entièrement la surface magnétique autour de laquelle elle s'enroule
au fil de ses passages successifs.
Ceci est vrai sauf dans le cas d'un
facteur de sécurité rationnel (c'est à dire égal au rapport de deux nombres
entiers) . Dans ce cas particulier, la ligne de champ se referme sur elle-même
au bout d'un nombre entier de tours, ce qui confère à la surface magnétique
des propriétés spécifiques (modification locale du transport, déclenchement
d'instabilités, ...)
Enfin, il est
à noter qu'en première approximation, les grandeurs macroscopiques (densité,
température, pression ...) sont homogènes sur une surface magnétique. On peut
donc les décrire dans une section poloïdale simplement en fonction du rayon du
plasma, par exemple en prenant leur valeur sur chaque cercle blanc illustrant
une surface magnétique sur le schéma ci-dessous. On
parle de profil radial (ne dépendant que du rayon), qui est dans le cas de la
densité, de la température et de la pression maximales au centre du
plasma et décroissent vers le bord de la décharge, comme illustré sur la
figure ci-dessous.
|
|
