Critčre de Lawson : la démonstration ...

L’énergie thermique d’un plasma D-T est :

   (k = constante de Boltzmann)

En supposant de plus :
que notre plasma est un mélange contenant 50% de Deutérium et 50% de Tritium
        et en tenant de la quasi-neutralité du plasma :
        n_D = n_T 
        n_ions = n_D + n_T = n 
        donc  n_D = n_T = n/2
une température uniforme T (T_électrons=T_ions=T)

On a : W = 3 nkT V (eq1)

La puissance fusion est égale aux nombres de réaction de fusion multipliée par
l'énergie dégagée par une réaction de fusion : P_fusion  = N_fusion  x E_fusion
or :
 
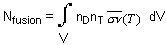
 sn(T) = taux de réaction ~ Cst T^˛  dans la gamme 10-20 keV (eq2)

d'oů : N_fusion = n˛ / 4  sn(T) V 

et P_fusion  = n˛ / 4  sn(T) V  E_fusion (eq3)

Reprenons notre bilan d'énergie. A l'état stationnaire (dW/dt = 0) , on a :

P_alpha + P_extérieure = P_pertes = W/ t_E

Remplaçons  P_extérieure par P_fusion /Q. On obtient :
P_alpha + P_fusion /Q = W/ t_E ou encore P_fusion ( P_alpha /P_fusion + 1/Q ) = W/ t_E 

Or : P_alpha /P_fusion= E_alpha /E_fusion d'oů : 
P_fusion ( E_alpha /E_fusion + 1/Q ) = W/ t_E 

En remplaçant W et P_fusion par leur expression respective (eq1 et eq3), on obtient :
n˛ / 4  sn(T) V  E_fusion ( E_alpha /E_fusion + 1/Q ) = 3 nkT V/ t_E 

d'oů :

Application numérique :

k = 1 si Température et Energie sont en keV
E_fusion = 17.59 MeV = 17590 keV 
E_alpha = 3.56 MeV = 3560 keV
Q=Ą (ignition)
Entre 10 et 20 keV on a : sn(T) ~ 1.18 10^-24 T² m^-3s^-1 (T en keV)
d'oů :