Lawson’s criterion: the demonstration...

The thermal energy of a D-T plasma is:

   (k = Boltzmann’s constant)

Supposing in addition:
that our plasma is a mixture containing 50% Deuterium and 50% Tritium
and by obtaining from the plasma’s near neutrality :
        n_D = n_T 
        n_ions = n_D + n_T = n 
        thus  n_D = n_T = n/2
a uniform temperature T (T_électrons=T_ions=T)

We have : W = 3 nkT V (eq1)

The fusion power is equal to the number of fusion reactions multiplied by
The energy given off by a fusion reaction : P_fusion  = N_fusion  x E_fusion
thus :
 
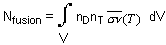
 sn(T) = reaction rate ~ Cst T^²  in the range 10-20 keV (eq2)

hence : N_fusion = n² / 4  sn(T) V 

and P_fusion  = n² / 4  sn(T) V  E_fusion (eq3)

Let us go back to our energy balance. In a stable state (dW/dt = 0) , we have :

P_alpha + P_external = P_losses = W/ t_E

Let us replace P_external by P_fusion /Q. We obtain :
P_alpha + P_fusion /Q = W/ t_E or even P_fusion ( P_alpha /P_fusion + 1/Q ) = W/ t_E 

Thus : P_alpha /P_fusion= E_alpha /E_fusion hence : 
P_fusion ( E_alpha /E_fusion + 1/Q ) = W/ t_E 

By replacing W and P_fusion by their respective expression nt>(eq1 et eq3), we obtain :
n² / 4sion  sn(T) V  E_fusion ( E_alpha /E_fusion + 1/Q ) = 3 nkT V/ t_E